Be yourself; Everyone else is already taken.
— Oscar Wilde.
This is the first post on my new blog. I’m just getting this new blog going, so stay tuned for more. Subscribe below to get notified when I post new updates.
Education mathematics
Be yourself; Everyone else is already taken.
— Oscar Wilde.
This is the first post on my new blog. I’m just getting this new blog going, so stay tuned for more. Subscribe below to get notified when I post new updates.






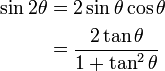
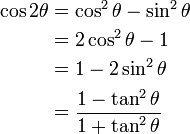
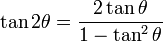
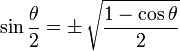
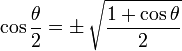
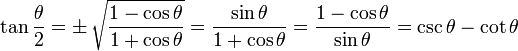
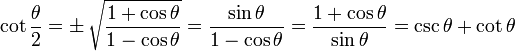
 means you can use plus or minus, and the
means you can use plus or minus, and the  means to use the opposite sign.
means to use the opposite sign. B) = sin(A)cos(B)
B) = sin(A)cos(B)  cos(A)sin(B)
cos(A)sin(B) B) = cos(A)cos(B)
B) = cos(A)cos(B)  sin(A)sin(B)
sin(A)sin(B) B) = tan(A) tan(B)1 tan(A)tan(B)
B) = tan(A) tan(B)1 tan(A)tan(B) B) = cot(A)cot(B) 1cot(B) cot(A)
B) = cot(A)cot(B) 1cot(B) cot(A)Here you can find a summary of the main formulas you need to know. This list was not organized by years of schooling but thematically. Just choose one of the topics and you will be able to view the formulas related to this subject. This is not an exhaustive list, ie it’s not here all math formulas that are used in mathematics class, only those that were considered most important.
| area | |||
| Square | A=l2A=l2 | ll : length of side | |
| Rectangle | A=w×hA=w×h | ww : width hh : height | |
| Triangle | A=b×h2A=b×h2 | bb : base hh : height | |
| Rhombus | A=D×d2A=D×d2 | DD : large diagonal dd : small diagonal | |
| Trapezoid | A=B+b2×hA=B+b2×h | BB : large side bb : small side hh: height | |
| Regular polygon | A=P2×aA=P2×a | PP : perimeter aa : apothem | |
| Circle | A=πr2A=πr2 P=2πrP=2πr | rr : radius PP : perimeter | |
| Cone (lateral surface) | A=πr×sA=πr×s | rr : radius ss : slant height | |
| Sphere (surface area) | A=4πr2A=4πr2 |
| Cube | V=s3V=s3 | ss: side | |
| Parallelepiped | V=l×w×hV=l×w×h | ll: length ww: width hh: height | |
| Regular prism | V=b×hV=b×h | bb: base hh: height | |
| Cylinder | V=πr2×hV=πr2×h | rr: radius hh: height | |
| Cone (or pyramid) | V=13b×hV=13b×h | bb: base hh: height | |
| Sphere | V=43πr3 |
| Directly Proportional | y=kxy=kx k=yxk=yx | kk: Constant of Proportionality |
| Inversely Proportional | y=kxy=kx k=yxk=yx | |
| ax2+bx+c=0ax2+bx+c=0 | Quadratic formula | x=−b±b2−4ac−−−−−−−√2ax=-b±b2-4ac2a |
| Concavity | Concave up: a>0a>0 | |
| Concave down: a<0a<0 | ||
| Discriminant | Δ=b2−4acΔ=b2-4ac | |
| Vertex of the parabola | V(−b2a,−Δ4a)V(-b2a,-Δ4a) | |
| y=a(x−h)2+ky=a(x-h)2+k | Concavity | Concave up: a>0a>0 |
| Concave down: a<0a<0 | ||
| Vertex of the parabola | V(h,k)V(h,k) | |
| Zero-product property | A×B=0⇔A=0∨B=0A×B=0⇔A=0∨B=0 | ex : (x+2)×(x−1)=0⇔(x+2)×(x-1)=0⇔ x+2=0∨x−1=0⇔x=−2∨x=1x+2=0∨x-1=0⇔x=-2∨x=1 |
| Difference of two squares | (a−b)(a+b)=a2−b2(a-b)(a+b)=a2-b2 | ex : (x−2)(x+2)=x2−22=x2−4(x-2)(x+2)=x2-22=x2-4 |
| Perfect square trinomial | (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2 | ex : (2x+3)2=(2x)2+2⋅2x⋅3+32=(2x+3)2=(2x)2+2⋅2x⋅3+32= 4×2+12x+94×2+12x+9 |
| Binomial theorem (x+y)n=∑k=0n nCk xn−k yk |
| Product | am×an=am+nam×an=am+n | ex : 35×32=35+2=3735×32=35+2=37 |
| am×bm=(a×b)mam×bm=(a×b)m | ex : 35×25=(3×2)5=6535×25=(3×2)5=65 | |
| Quotient | am÷an=am−nam÷an=am-n | ex : 37÷32=37−2=3537÷32=37-2=35 |
| am÷bm=(a÷b)mam÷bm=(a÷b)m | ex : 65÷25=(6÷2)5=3565÷25=(6÷2)5=35 ex : 53÷23=(52)353÷23=(52)3 | |
| Power of Power | (am)p=am×p(am)p=am×p | ex : (52)3=52×3=56(52)3=52×3=56 |
| Zero Exponents | a0=1a0=1 | ex : 80=180=1 |
| Negative Exponents | a−n=(1a)na-n=(1a)n | ex : 3−2=(13)23-2=(13)2 ex : (23)−4=(32)4(23)-4=(32)4 |
| Fractional Exponents | apq=ap−−√qapq=apq | ex : 243=24−−√3243=243 |

This is an example post, originally published as part of Blogging University. Enroll in one of our ten programs, and start your blog right.
You’re going to publish a post today. Don’t worry about how your blog looks. Don’t worry if you haven’t given it a name yet, or you’re feeling overwhelmed. Just click the “New Post” button, and tell us why you’re here.
Why do this?
The post can be short or long, a personal intro to your life or a bloggy mission statement, a manifesto for the future or a simple outline of your the types of things you hope to publish.
To help you get started, here are a few questions:
You’re not locked into any of this; one of the wonderful things about blogs is how they constantly evolve as we learn, grow, and interact with one another — but it’s good to know where and why you started, and articulating your goals may just give you a few other post ideas.
Can’t think how to get started? Just write the first thing that pops into your head. Anne Lamott, author of a book on writing we love, says that you need to give yourself permission to write a “crappy first draft”. Anne makes a great point — just start writing, and worry about editing it later.
When you’re ready to publish, give your post three to five tags that describe your blog’s focus — writing, photography, fiction, parenting, food, cars, movies, sports, whatever. These tags will help others who care about your topics find you in the Reader. Make sure one of the tags is “zerotohero,” so other new bloggers can find you, too.